Big-Oh: Mathematical Definition
- Express the mathematical definition of Big-Oh.
$$ T(n) \in \Omicron(f(n))\Leftrightarrow \exists \; c > 0, n_0 > 0 \; \; s.t. \; \; T(n) \le c\cdot f(n) \; \; \forall \; n \ge n_0 $$
Read it as
$T(n)$ is a member of $\Omicron(f(n))$ if and only if there exist positive constants $c$ and $n_0$ such that $T(n)\le c\cdot f(n)$ for all $n\ge n_0$.
Here is a pictorial illustration of the above definition:
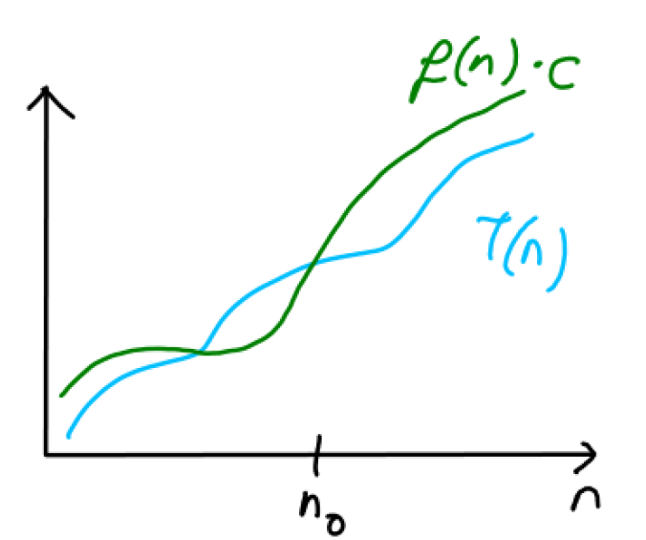
If you want to show that $T(n) \in \Omicron(f(n))$, you need to choose the constants $c$ and $n_0$ so that above definition holds whenever $n \ge n_0$.
Exercise The running time of an algorithm is $T(n)=7n^2+5$. Show that this algorithm has quadratic runtime, i.e., show $T(n) \in \Omicron(n^2)$.
Solution
We can choose $c=12$ and $n_0=1$ for the definition of Big-Oh to hold.
There is not a magic formula to find the constants. However, you can usually guess the values or deduct them by simple algebraic modification of $T(n)$.
$$ T(n) = 7n^2 + 5 \le 7n^2 + 5n^2 \le 12n^2 $$
Please note the choice of $n_0$ and $c$ are not unique. Moreover, these constants are not necessarily integers. According to the definition, these constants are non-zero and positive real values. Of course, if $n$ represents the program input size, then it is imperative to be an integer.
Please also note I have deliberately asked you to "show" $T(n) \in \Omicron(n^2)$ and not "to prove." However, a proof generally would require finding a pair of $c$ and $n_0$ for the definition to hold. Of course, you should present your argument more formally. For example, the following would make reasonable proof. Notice I deliberately chose a different pair of $c$ and $n_0$ from those selected above.
Proof: Let's set $c = 10$. Now suppose that $7n^2 + 5 > 10n^2$. Then by algebraic simplification, we get $3n^2 < 5$, and thus $-\sqrt{\frac{5}{3}} < n < \sqrt{\frac{5}{3}}$. So by the counterpositive, $7n^2 + 5 \le 10n^2$ for all $n \ge \sqrt{\frac{5}{3}}$. So if we set $n_0 = \left \lceil \sqrt{\frac{5}{3}} \right \rceil = 2$, we have proved that $7n^2 + 5 \le cn^2$ for $c = 10$ for all $n > n_0$. Thus we have proved that $T(n) \in \Omicron(n^2)$. Q.E.D.
Resources
- Khan academy's article on Big O notation.
- Wikipedia's entry on Big O notation.
- This article is well written: Big-O Notation — A Primer.