Exercise IV

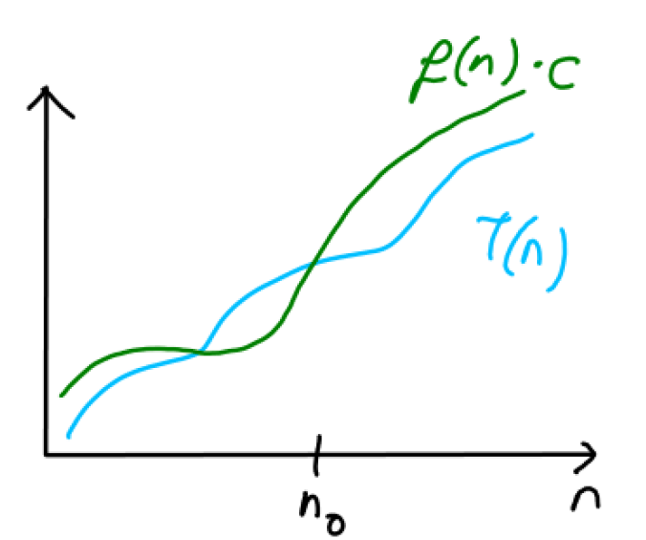
Consider the following facts:

• Baby chicken might be larger than baby turkey at the beginning.
• But after a certain "breakpoint," the chicken size will be surpassed by the turkey size.
• From the breakpoint on, the chicken size will always be smaller than the turkey size.

Exercise Which statement is true?

A) chicken size is in $\Omicron($turkey size$)$.
B) turkey size is in $\Omicron($chicken size$)$.

Solution

Chicken's growth order is smaller than turkey's, or chicken size is in $\Omicron($turkey size$)$.

The breakout point is the $n_0$ in the mathematical definition of Big-Oh.