Dynamic Connectivity

  • Identify the operations of the Dynamic Connectivity structure.

Kruskal's algorithm needs a data structure that dynamically (and efficiently) maintains information about the connected components of a graph.

Why does Kruskal's algorithm need such a data structure?

Every edge selected by Kruskal's algorithm must be checked to ensure adding it to the MST would not create a cycle. If the two endpoints of the edge are already "connected" (i.e. there is a path between them), adding the edge will create a cycle.

Such a data structure is called Dynamic Connectivity structure. According to Wikipedia:

In a dynamic connectivity structure, the set VV of vertices of the graph is fixed, but the set EE of edges can change:

  • Edges may only be added to the graph (incremental connectivity);
  • Edges may only be deleted from the graph (decremental connectivity);
  • Edges can be either added or deleted (fully dynamic connectivity).

After each addition/deletion of an edge, the dynamic connectivity structure should adapt itself to answer questions such as "is there a path between xx and yy? or equivalently: "do vertices xx and yy belong to the same connected component?".

For example, consider the following graph:

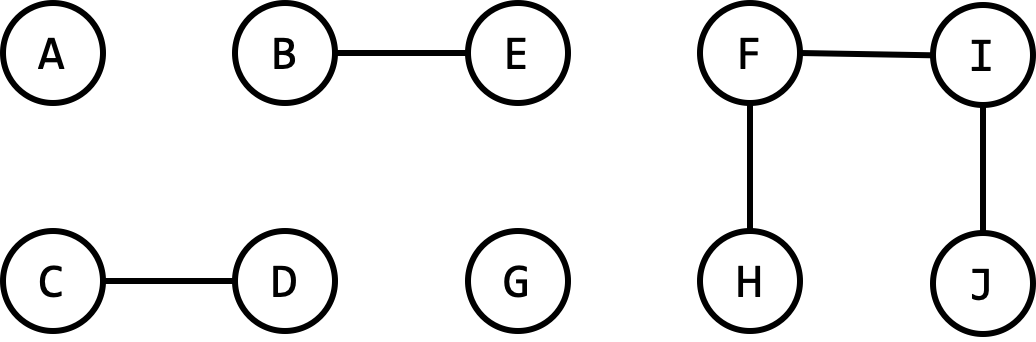
We may ask if there is a path between vertices AA and GG? Or if the vertices HH and JJ belong to the same connected component?

connected(A,G)  // false
connected(H,J)  // true
Notice "is connected to" is an equivalence relation
  • Reflexive: pp is connected to pp.
  • Symmetric: if pp is connected to qq, then qq is connected to pp.
  • Transitive: if pp is connected to qq and qq is connected to rr, then pp is connected to rr.

If edges can only be added, then the dynamic connectivity problem can be solved by a Union-Find data structure.

Resources