In-order Traversal: Left, Root, Right!

  • Explain in-order traversal.

In a BST, in-order traversal will produce the sequence in order (duh!). In a way, we recreate the ordered sequence where this binary (decision) tree was generated from:

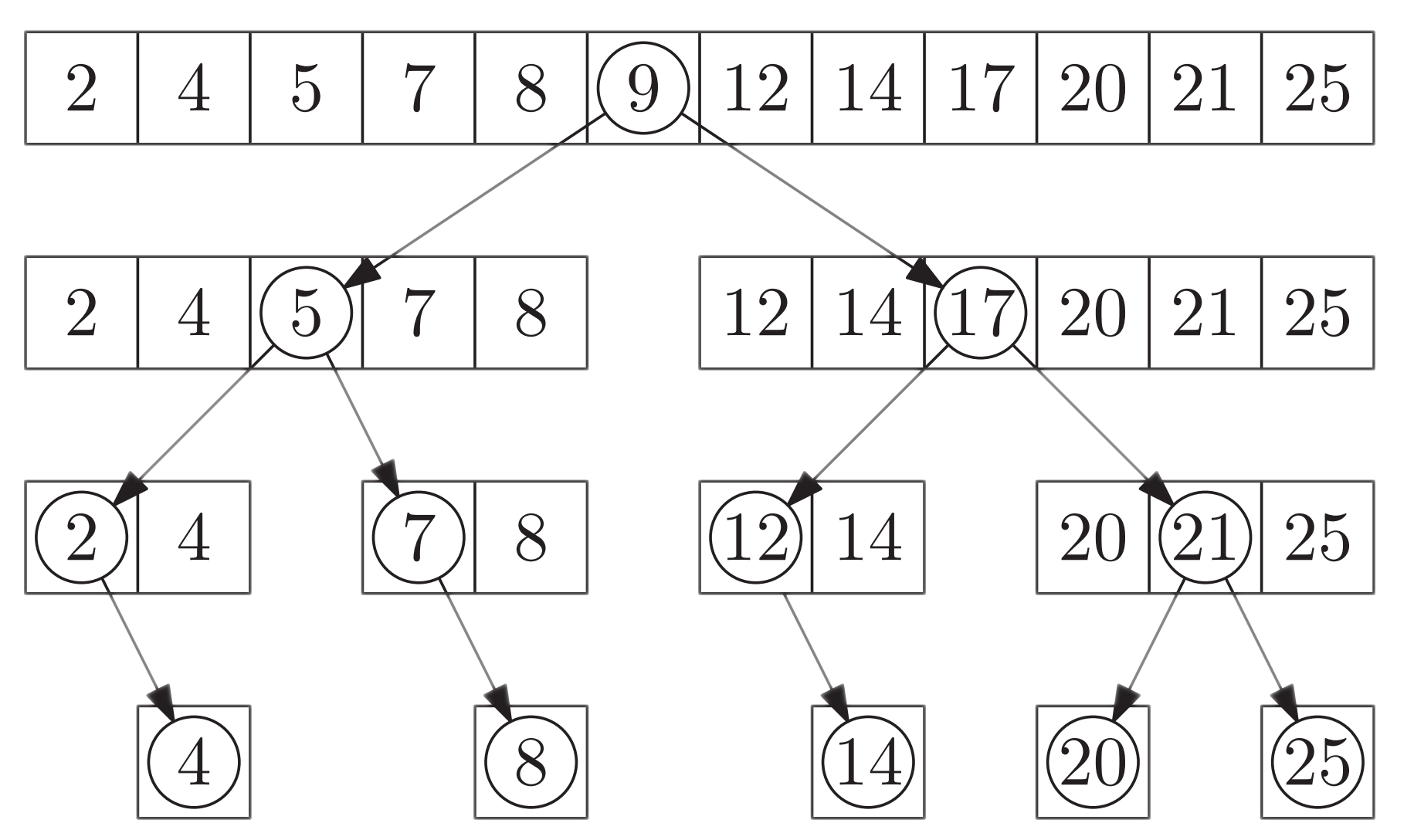
This is the strategy:

For every node, visit the left subtree, then the node, then the right subtree.

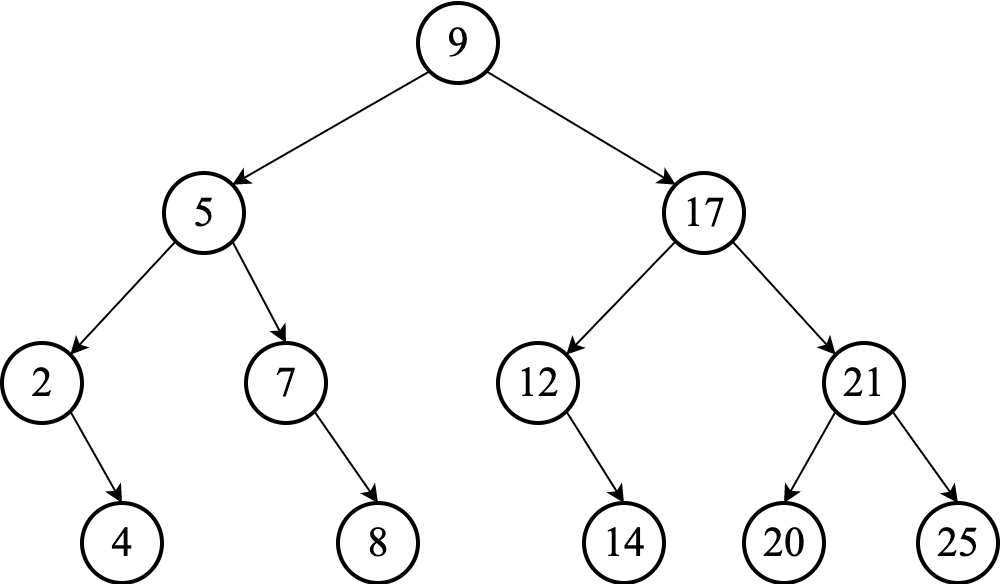
Following the strategy above will generate this sequence:

2,4,5,7,8,9,12,14,17,20,21,25 2, 4, 5, 7, 8, 9, 12, 14, 17, 20, 21, 25

Explanation

We start with the root, 99, but the strategy demands us to visit all the nodes in the left subtree first. So we move to the subtree rooted at 55. However, before we visit 55, we must visit all the nodes in its left subtree. So we move to the subtree rooted at 22. Since there is no subtree to the left of 22, we can visit 22. Thus the first node that we will iterate over is going to be 22.

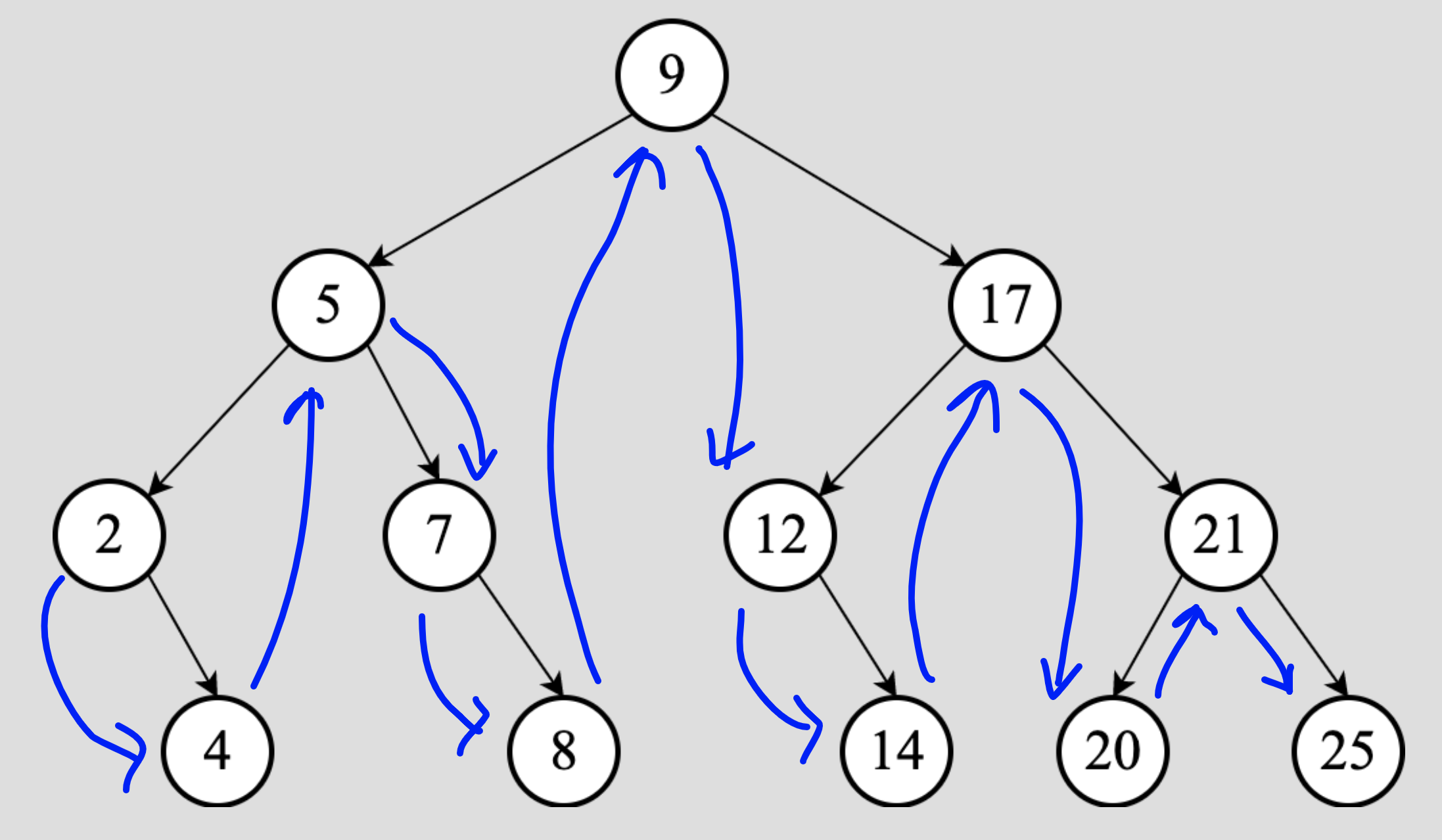
According to the strategy, when a node is visited, we must visit all the nodes in its right subtree. So we move to node 44. We must visit all the nodes in the subtree to the left of 44, but there are none, so we can process 44 itself. Therefore, 44 will be the second node we will iterate over. We must now visit all the nodes to the right subtree of 44, but there is none. Therefore, we conclude our visit of all the nodes in the right subtree of 22, and by proxy, our visit to all the nodes in the left subtree of 55 is done too. We must now process 55 itself. Thus, 55 will be the third node we will iterate over. Then we move to the right subtree of 55 and …\dots

Here is a recursive definition of in-order traversal: for each node, recursively perform in-order traversal of the subtree rooted at its left child, then visit the root (the note itself), then recursively perform in-order traversal of the subtree rooted at its right child.

Resources