Big Theta

  • Express the mathematical definition of Big Theta.

Big Theta is used to describe asymptotic tight bound!

T(n)∈Θ(f(n))⇔∃  c1>0,c2>0,n0>0 T(n) \in \Theta(f(n))\Leftrightarrow \exists \; c_1 > 0, c_2 > 0, n_0 > 0

s.t.    c1⋅f(n)≤T(n)≤c2⋅f(n)    ∀  n≥n0 s.t. \; \; c_1\cdot f(n) \le T(n) \le c_2\cdot f(n) \; \; \forall \; n \ge n_0

Read it as

T(n)T(n) is a member of Θ(f(n))\Theta(f(n)) if and only if there exist positive constants c1c_1, c2c_2 and n0n_0 such that c1⋅f(n)≤T(n)≤c2⋅f(n)c_1\cdot f(n) \le T(n)\le c_2\cdot f(n) for all n≥n0n\ge n_0.

Θ(f(n))\Theta(f(n)) is the set of functions that grow no faster and no slower than f(n)f(n).

Here is a pictorial illustration of the above definition:

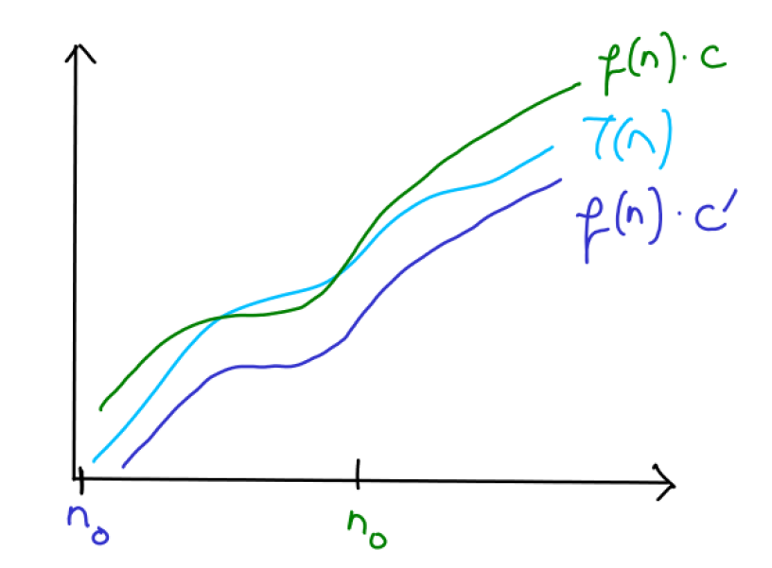
If you want to show that T(n)∈Θ(f(n))T(n) \in \Theta(f(n)), you need to choose the constants c1c_1, c2c_2, and n0n_0 so that above definition holds whenever n≥n0n \ge n_0.

Exercise The running time of an algorithm is T(n)=7n2+5T(n)=7n^2+5. Show that T(n)∈Θ(n2)T(n) \in \Theta(n^2).

Solution

We can choose c1=7c_1=7, c2=12c_2=12, and n0=1n_0=1 for the definition of Big Theta to hold.

7n2≤7n2+5≤12n2 7n^2 \le 7n^2 + 5 \le 12n^2

Please note, another way of defining Big Theta is as follows:

T(n)∈Θ(f(n))T(n) \in \Theta(f(n)) if and only if T(n)∈O(f(n))T(n) \in \Omicron(f(n)) and T(n)∈Ω(f(n))T(n) \in \Omega(f(n)).

Note that Big Theta describes a tight bound. So it is a stronger statement than Big-Oh and big Omega.

Resources