In the decision tree corresponding to the comparison-based sorting algorithm, the number of leaves is greater or equal to the number of possible answers which is greater or equal to $n!$, the number of permutations of the elements.

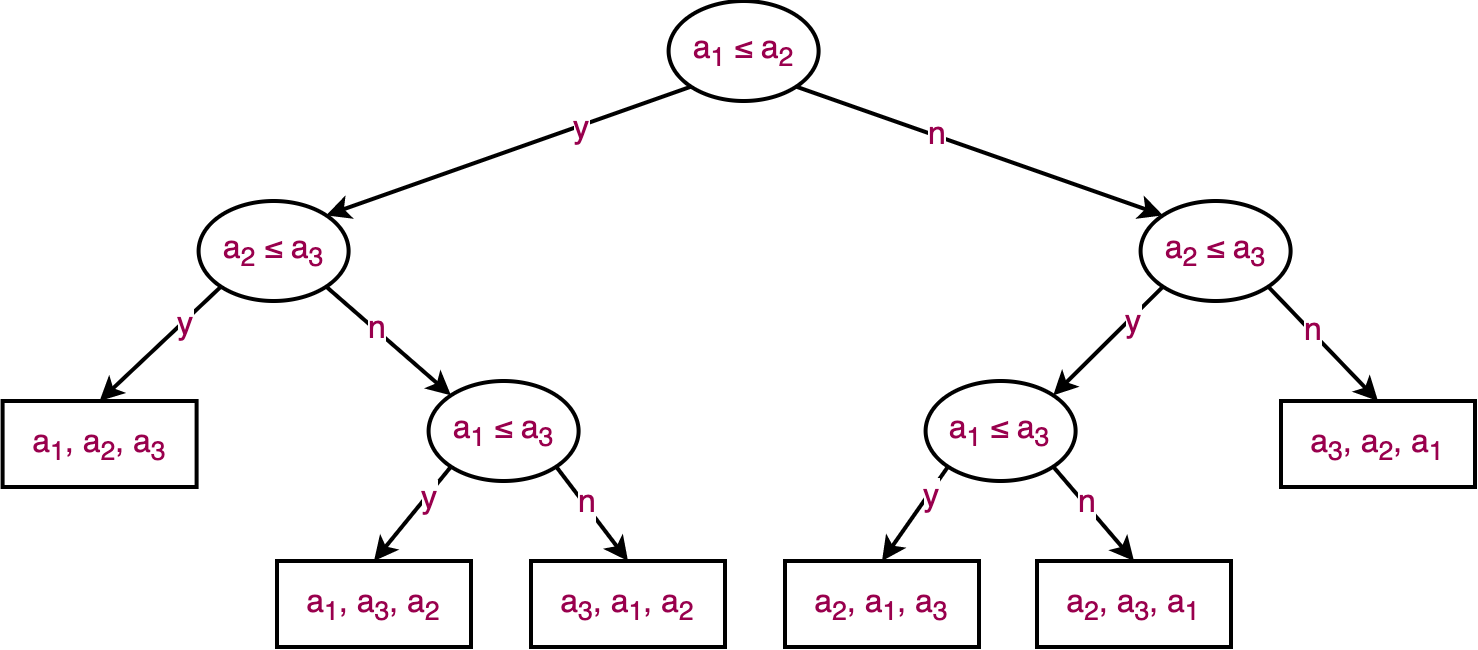
As it can be seen in the diagram above, for a collection with $3$ elements, there are $3!=6$ permutations in which one is the correct answer (elements in sorted order; there is only one sorted order if elements are unique).

Expand $n!$

$$\lg n! = \lg(1\times 2 \times \dots \times n) = \lg 1 + \lg 2 + \dots + \lg n$$

If we take out $\lg 1 + \lg 2 + \dots$ up to but not including $\lg \frac{n}{2}$ from the above series, we have:

$$\lg \frac{n}{2} + \dots + \lg n \le \lg n!$$

We can also write

$$\lg \frac{n}{2} + \lg \frac{n}{2} + \dots + \lg \frac{n}{2} \le \frac{n}{2} \times \lg \frac{n}{2} \le \lg n!$$

Therefore $\lg n! \in \Omega(n \lg n)$.

Moreover, we can show $\lg n! \in \Omicron(n \lg n)$ because

$$\lg n! \le \lg 1 + \lg 2 + \dots + \lg n \le \lg n + \lg n + \dots \lg n \le n \times \lg n$$

So, in fact, $\lg n! \in \Theta(n \lg n)$.

Aside: You can also show this using Stirling's approximation:

$$n! \approx \sqrt{2\pi n} \left ( \frac{n}{e} \right )^n$$