Summary

Elaborate on the benefits of using asymptotic notation and worst-case analysis to study the computational complexity of algorithms.

The Big-Oh notation and worst-case analysis are tools that greatly simplify our ability to compare the efficiency of algorithms.

Asymptotic analysis means using asymptotic notation to describe the computational complexity of an algorithm.
Computational complexity generally means time complexity and space complexity.
If it is not specified, we mean time complexity.
If it is not specified, we mean worst-case analysis.
If it is not specified, we want Big-Oh notation.
When using Big-Oh, give the tightest upper bound you can find.
When using big Omega, give the tightest lower bound you can find.
If it is not specified, space complexity should include input and auxiliary space.

Notation	Definition
$\Omicron$	Big-Oh: $T(n)$ is a member of $\Omicron(f(n))$ if and only if there exist positive constants $c$ and $n_0$ such that $T(n)\le c f(n)$ for all $n\ge n_0$ .
$\Omega$	Big Omega: $T(n)$ is a member of $\Omega(f(n))$ if and only if there exist positive constants $c$ and $n_0$ such that $T(n)\ge c f(n)$ for all $n\ge n_0$ .
$\Theta$	Big Theta: $T(n)$ is a member of $\Theta(f(n))$ if and only if there exist positive constants $c_1$ , $c_2$ and $n_0$ such that $c_1 f(n) \le T(n) \le c_2 f(n)$ for $n\ge n_0$ .

The following illustration is taken from the bible of Algorithm, the CLRS book:

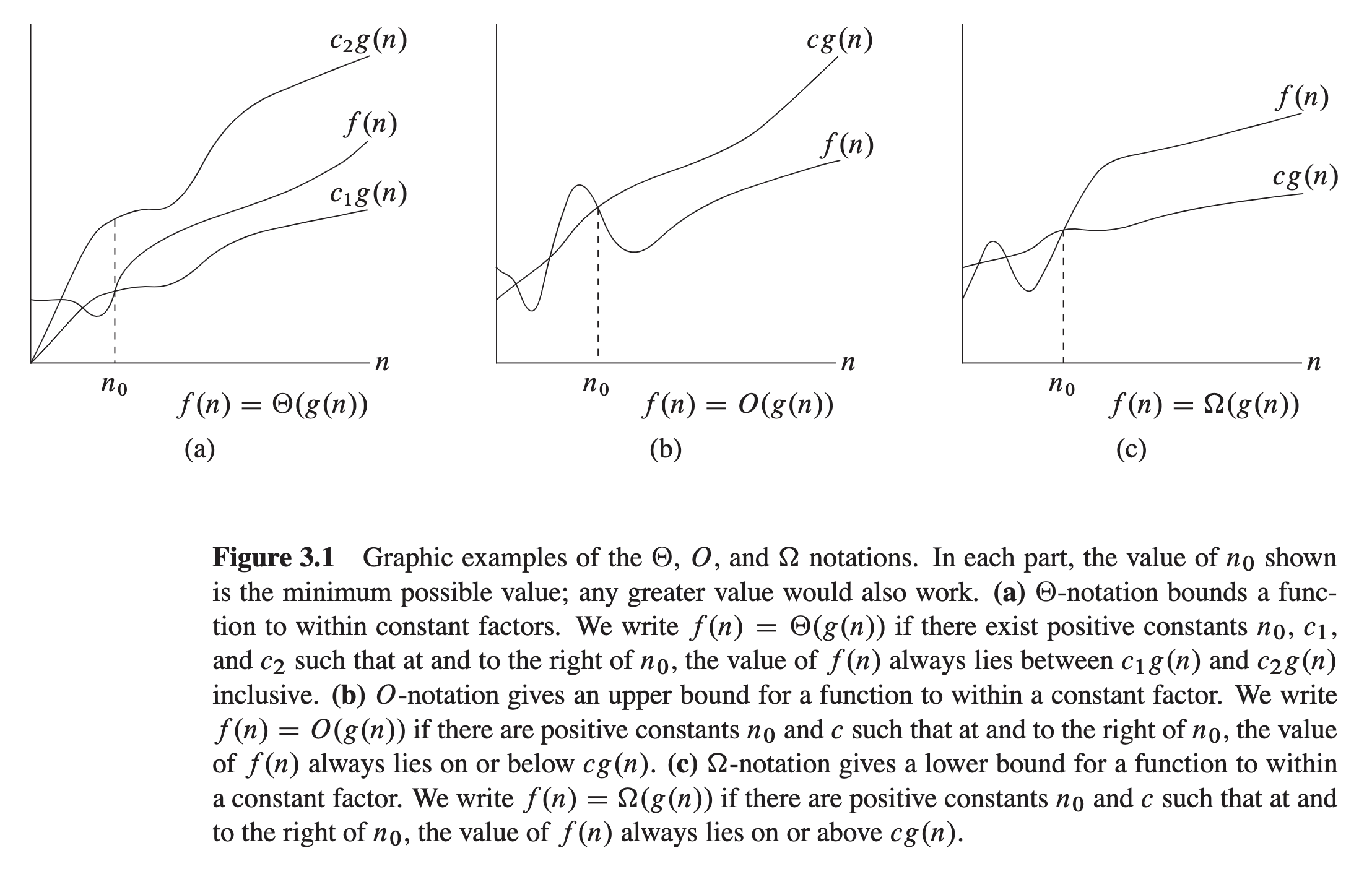
There are other asymptotic notations (Little Oh, Little Omega, etc.) which I have spared you the grief of knowing!

Resources

For a brief & concise overview, refer to any of the following:

Educative's short article on Time complexity vs space complexity
InterviewCake's article Big-O notation
HackerEarch's tutorial Time and Space Complexity
Cornell's cs3110 online lecture notes
MIT's 16.070 online lecture notes
Big-O notation in 5 minutes — The basics on YouTube.
Asymptotic Bounding 101: Big O, Big Omega, & Theta (Deeply Understanding Asymptotic Analysis on YouTube.
Online notes on Analysis of Algorithms accompanying Robert Sedgewick's book "Algorithms."
TowardsDataScience's article The Math Behind "Big O" and Other Asymptotic Notations

For an in-depth, detailed, formal (mathematical) discussion of asymptotic analysis, refer to chapter 3, "Growth of Functions," in CLRS: Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein, Introduction to Algorithms. 3rd ed, MIT Press, 2009.

Data Structures

Summary