Balance Factor

  • Identify the height and balance factor of binary search tree nodes.

To assist in establishing balance property, we define the following measure:

Each node's balance factor is the height of the left subtree minus the height of the right subtree.

More specifically

bf(node) = height(node.left) – height(node.right)

For the calculation of balance factor, we define "height" as follows:

height(n)={−1n=null0n=leaf1+max⁡(height of children)n≠leaf} \text{height}(n)=\left \{ \begin{matrix} -1 & n = \text{null} \\ 0 & n = \text{leaf} \\ 1 + \max(\text{height of children}) & n \neq \text{leaf} \end{matrix} \right \}

A BST is balanced when, for any node, its balance factor is 11, 00, or −1-1.

Here is an example

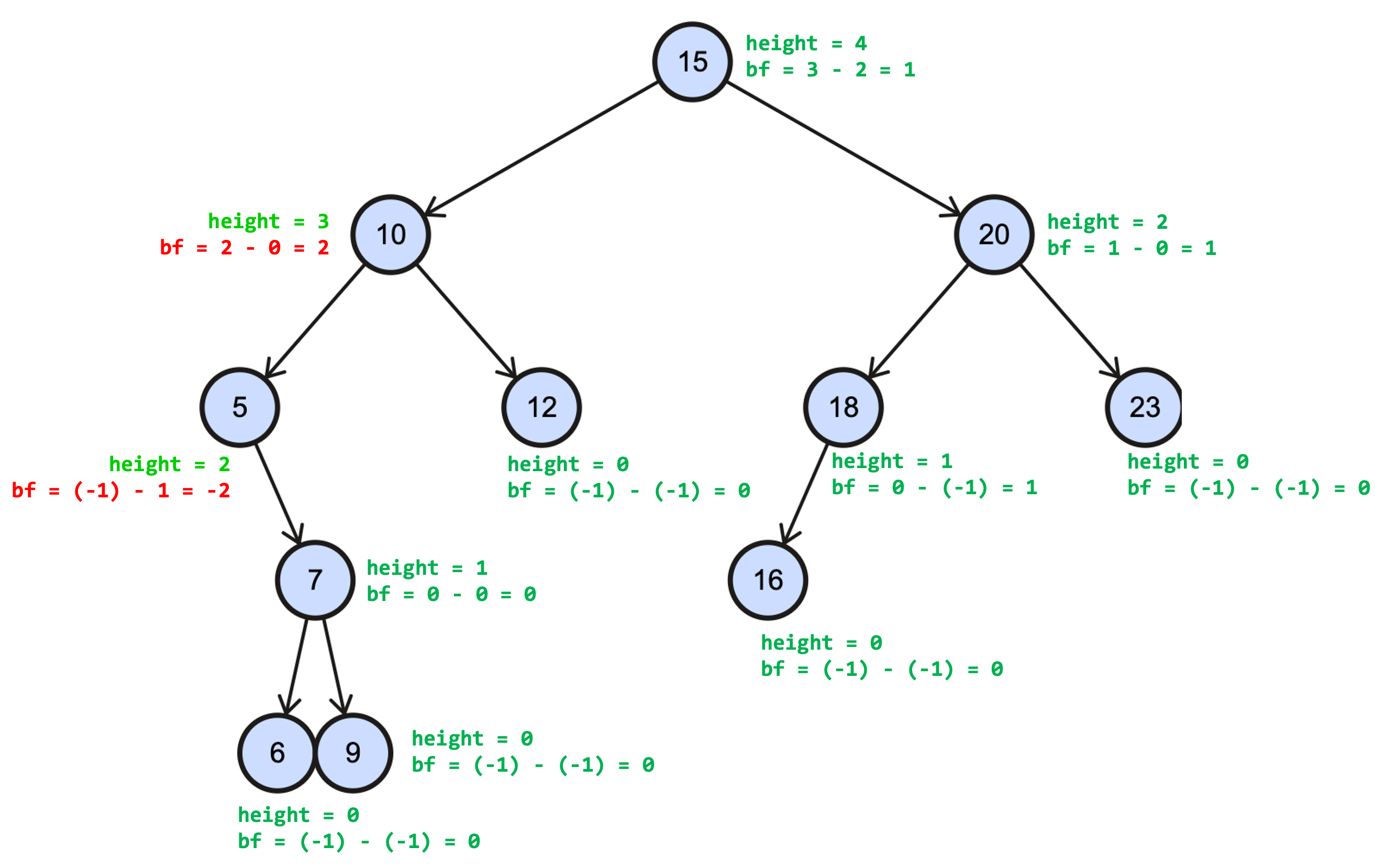
The above BST is not balanced because bf({10,5})∉{0,1,−1}\text{bf}(\{ 10, 5 \})\notin \{0, 1, -1 \}.