Chaining: Analysis
- Analyze the efficiency of "separate chaining" hash tables.
In chaining, insert, remove, and lookup, run proportional to the number of keys in the given chain. So, to analyze the complexity, we need to examine the length of the chains.
Best case: if we are lucky, the number of elements inserted is smaller than the capacity of the table, and we have a stellar hashing procedure with no collision! So the performance for insert, remove, and search are $\Omicron(1)$.
Worst case: if we're unlucky with the keys we encounter or have a poorly implemented hashing procedure, all keys may get mapped to the same bucket.

In the worst-case, the performance is $\Omicron(N)$ where $N$ is the number of items stored in the hash table. (Assuming the auxiliary is a linked list).
Average case: under the assumption of uniform hashing, we expect each bucket to be of size $\frac{N}{M}$ where $N$ is the number of items stored in the hash table, and $M$ is its size (number of array/table slots). Notice this ratio is the load factor. Therefore, the performance is $\Omicron(\alpha)$.
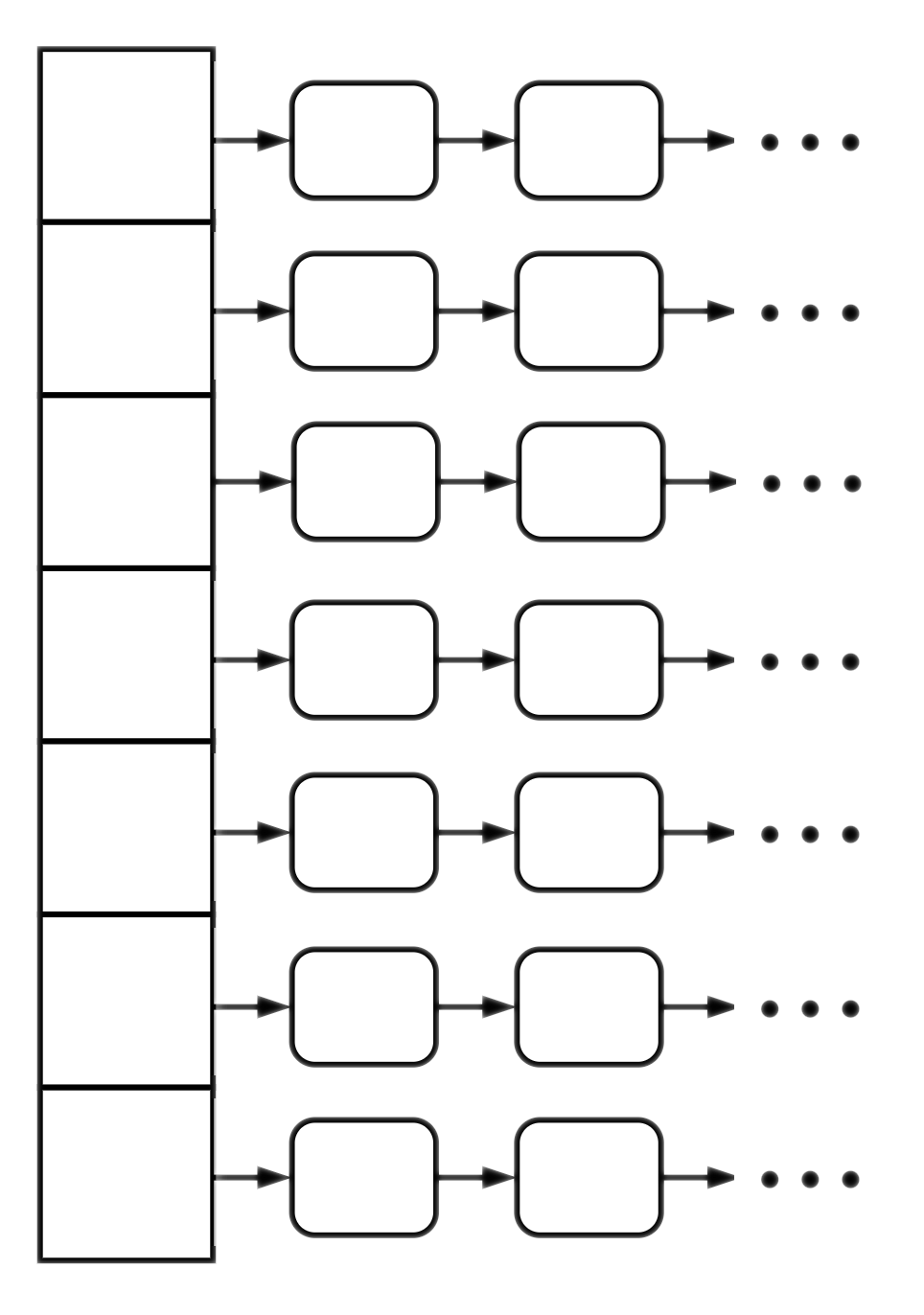
If we keep the $\alpha$ bounded by a small constant (preferably below $1$), we get (expected) constant runtime operations (in the average case analysis).
Notice that the performance also depends on the choice of the auxiliary data structures. The most common choices follow.
| Chaining in each bucket | find | delete | insert |
|---|---|---|---|
| (Unordered) linked list | $\Omicron(\alpha)$ | $\Omicron(\alpha)$ | $\Omicron(\alpha)$ |
| (Ordered) dynamic array | $\Omicron(\lg \alpha)$ | $\Omicron(\alpha)$ | $\Omicron(\alpha)$ |
| (Self-balancing) binary search tree | $\Omicron(\lg \alpha)$ | $\Omicron(\lg \alpha)$ | $\Omicron(\lg \alpha)$ |
In Java, the HashMap is implemented using a chaining strategy with a linked list auxiliary data structure. Java's HashMap maintains a load factor $\alpha \le 0.75$. When the number of elements is reached a certain limit, it switches to a BST for the auxiliary data structure (the keys must also be "comparable" otherwise you wouldn't be able to build BSTs).
Resources
- Wikipedia entry on Hash Table: Performance.