Right Rotation: Exercise IV
- Implement Single Right Rotation.
Consider the schematic representation of the pattern that leads to a (single) right rotation:
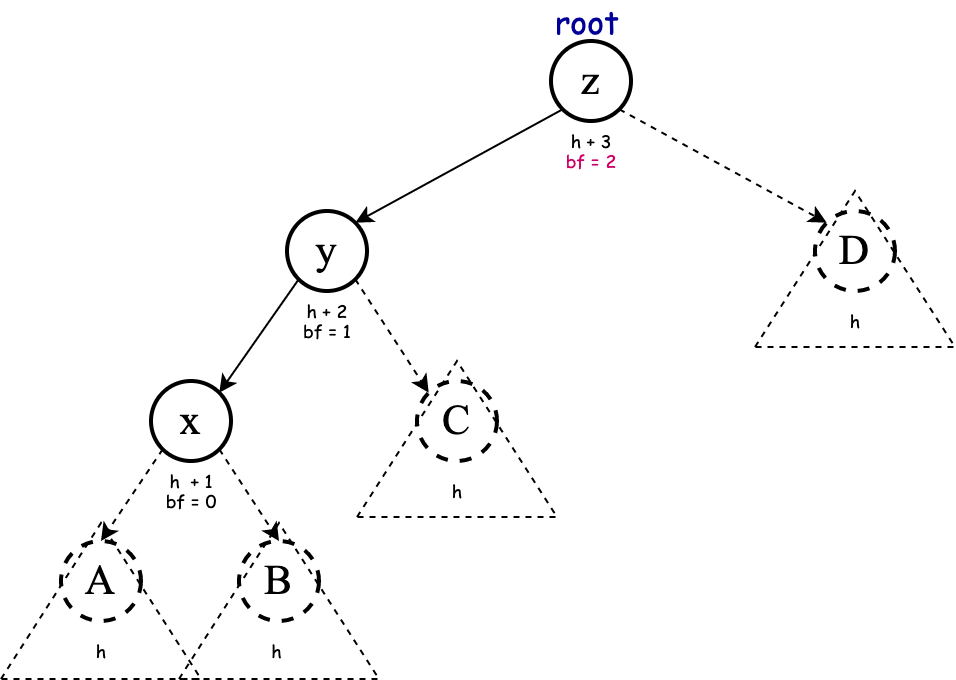
The nodes with dashed line are roots of their own subtree (they could be null too). After the application of right rotation, we get the following:
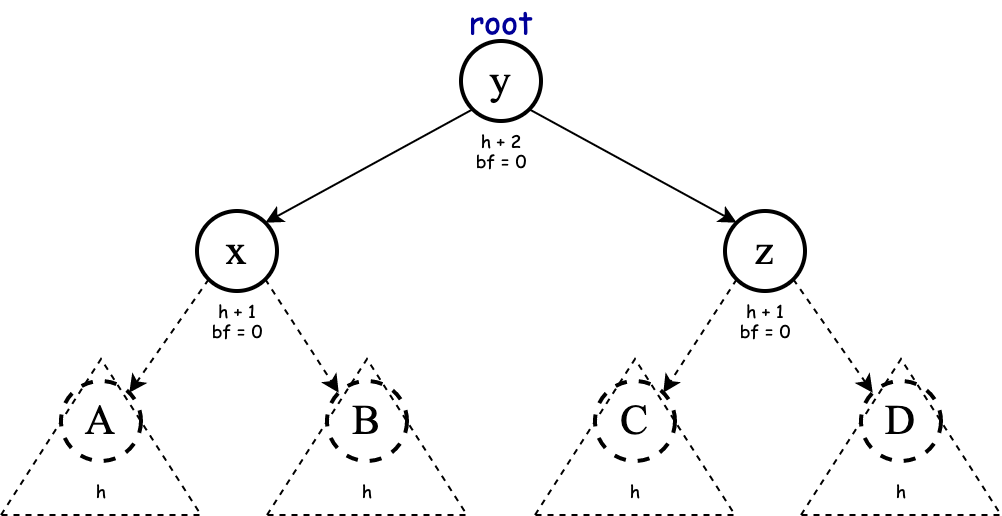
Exercise Complete the implementation of rightRotation method:
Node<T> rightRotation (Node<T> root) {
// TODO Implement me!
}
Note: The argument to rightRotation is the root of a subtree (not necessarily the root of the BST). The rightRotation must return the updated (new) root. Assume each node has access to its left/right subtrees.
Solution
Node<T> rightRotation (Node<T> root) {
Node<T> child = root.left;
root.left = child.right;
child.right = root;
return child;
}
Exercise What is the time complexity of your implementation of rightRotation method?
Solution
The rightRotation involves a constant number of assignments. Therefore, its time complexity is $\Omicron(1)$