Merge Sort: Analysis

  • Analyze the best and worst-case time efficiency of MergeSort.

The merge sort runs in O(nlg⁡n)\Omicron(n \lg n) time.

Justification:

  • The number of times the merge sort divides a sequence is the number of times nn can be halved: O(lg⁡n)\Omicron(\lg n). Therefore, the divide part has O(lg⁡n)\Omicron(\lg n) levels. At each level ll, we perform 2l2^l divide (which itself is a constant time). So the total work is 20+21+⋯+2lg⁡n∈O(n)2^0 + 2^1 + \dots + 2^{\lg n} \in \Omicron(n).
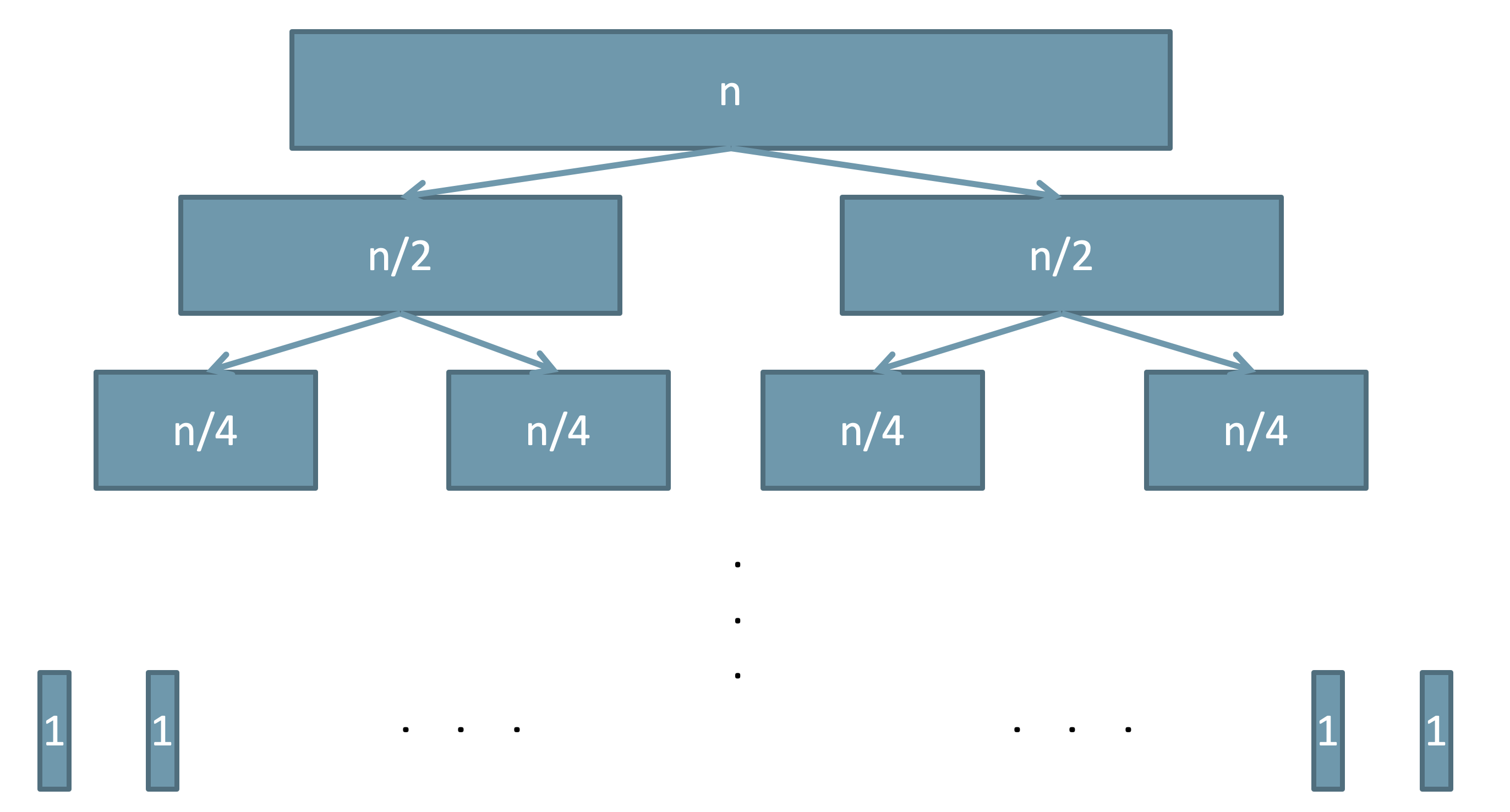
  • The number of times merge sort merges the subsequences is equal to the number of sub-sequences. Therefore, the merging part also has O(lg⁡n)\Omicron(\lg n) levels. Consider at each level, we perform k×O(n/k)∈O(n)k\times \Omicron(n/k) \in \Omicron(n) time to merge the sub-arrays. So the total running time for the merge sort algorithm is O(nlg⁡n)\Omicron(n \lg n),
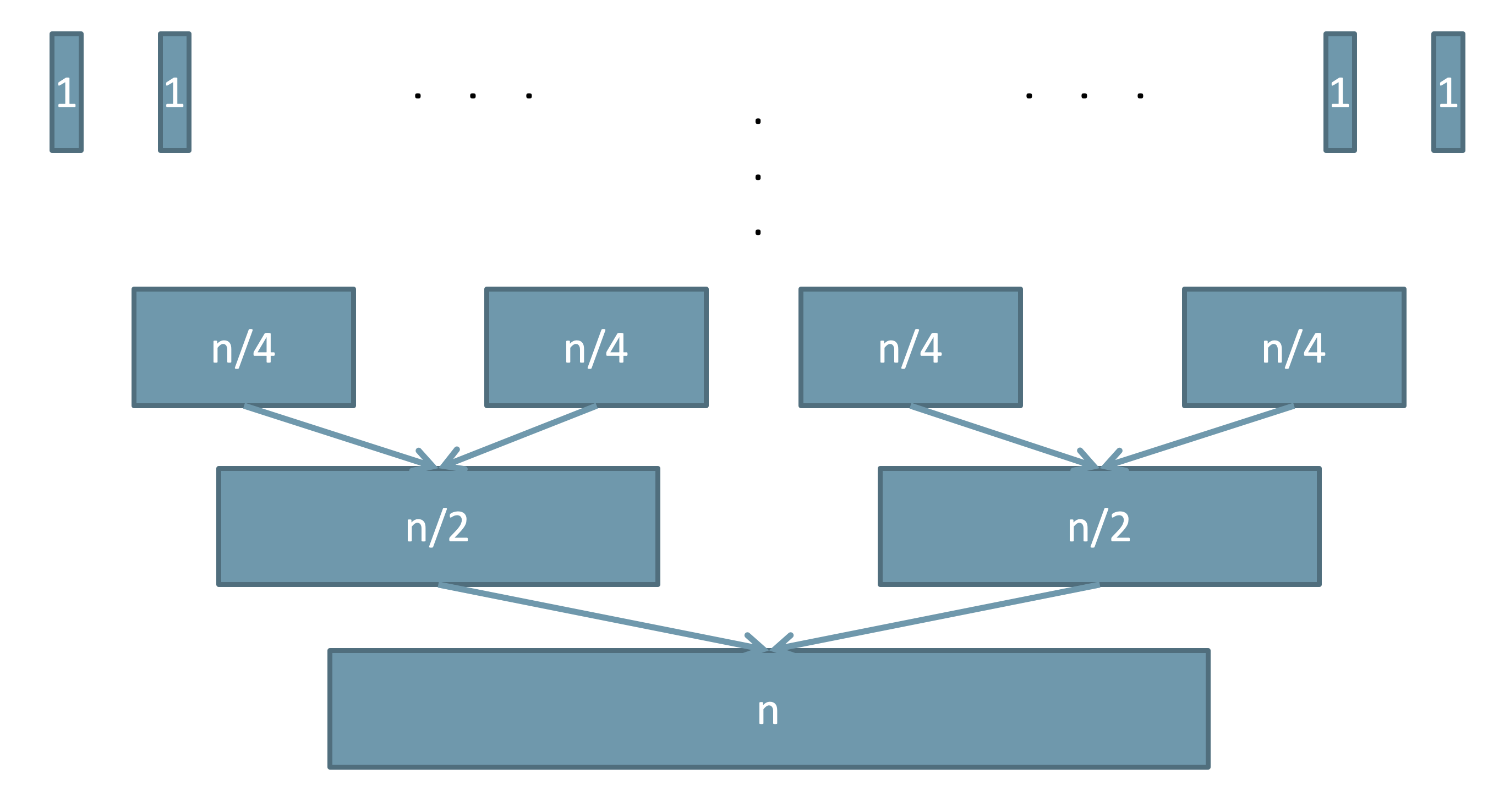
Formal Proof

A formal proof can be constructed by writing the runtime of merge sort as a recurrence relation T(n)=2T(n/2)+θ(n)T(n) = 2T(n/2) + \theta(n) and showing T(n)∈θ(nlg⁡n)T(n) \in \theta(n \lg n).

If you want to look this up, search for "the master theorem for divide-and-conquer recurrences" and look up "case 2". This is, however, beyond the scope of this course.

Resources